
BFS는 가중치가 없는 균일 그래프에서 최단경로를 계산하는 반면, 다익스트라 알고리즘은 가중치가 있는 그래프에서 최단 거리를 계산하는 데 사용된다.
아래 그림은 균일 그래프이다. 1번 vertex에서 출발하여 4번 vertex에 도착하기까지의 최단경로는 A, B 둘 중의 하나이다.
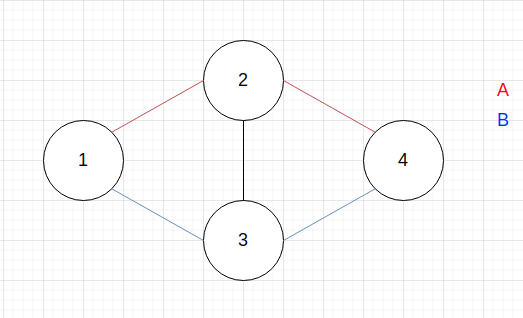
그렇다면 가중치가 있는 경우는 어떨까?
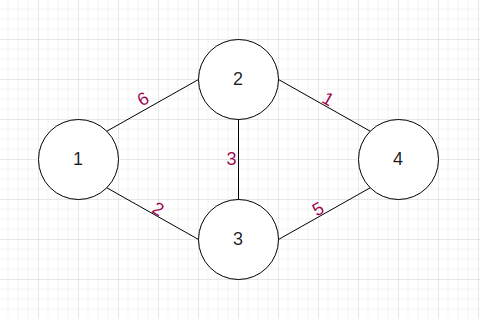
아까의 A경로 혹은 B경로 모두 7이라는 가중치를 가진다. 그런데, 우리는 직관적으로 더 짧은 길이 있음을 알 수 있다.
아래 그림의 화살표를 따라 이동하면, 가중치 6만에 도착할 수 있다.
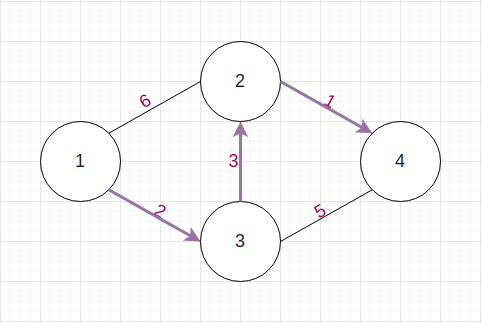
대체 가중치가 뭐길래?
쉽게 이해하자.
1번은 서울이고, 4번은 부산이다.
2번은 울산이고,
3번은 대전이다.
그래프의 간선에 표기된 가중치는, 현실 시간으로 30분이라고 가정하자.
서울에서 부산까지 가기 위해 기존의 방식대로 A 경로 ( 서울 -> 울산 -> 부산 )를 선택하면 3시간 30분이 걸린다.
마찬가지로 기존의 B 경로 ( 서울 -> 대전 -> 부산 )를 선택하면 3시간 30분이 걸린다.
그러나 새로운 경로 ( 서울 -> 대전 -> 울산 -> 부산 )를 따라 이동하면 3시간이면 목적지에 도착하는 것이다!!!
이렇게 가중치에 따라 우리가 원하는 최적의 결과를 찾는 것. 그게 다익스트라 알고리즘의 핵심이다.
Dijkstra's algorithm ( 다익스트라 알고리즘 )
우선, 위에서 예를 든 그림의 잘못된 점을 수정하고 가자.
다익스트라 알고리즘은 방향성 비순환 그래프 ( DAG, Directed Acyclic Graph ) 또는 사이클을 가진 경우 가중치가 양수일 때에만 적용이 된다.
다익스트라 알고리즘을 더 쉽게 이해하기 위해 또 그림을 가져왔다.
이번에는 우리 동네를 그렸다.
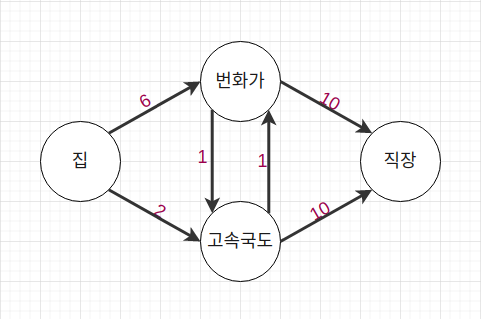
우리집에서 직장까지 가는 최단경로는 어떻게 가는 것일까?
다익스트라 알고리즘은 현재위치에서 이웃까지 도달하는 데 걸리는 시간을 계산하고, 그 중 최적의 값을 찾는다. 여기서는 시간이 짧은 것이 최적의 값이므로, 집에서 출발할 때에는 고속국도를 선택한다.
| 집 | 번화가 | 6 |
| 집 | 고속국도 | 2 |
다음은 고속국도에서 이웃까지 도달하는 데 걸리는 시간이다.
| 집 | 고속국도 | 2 |
| 고속국도 | 번화가 | 1 |
| 고속국도 | 직장 | 10 |
우리는 직장까지 가야하기때문에 현재 집에서 직장까지의 가중치는 총 12이다. ( 집 -> 고속국도 -> 직장 )
그런데 여기! 고속국도에서 번화가로 가중치 1만에 이동할 수 있다! 그래서 이번에는 번화가로 이동한다!
| 집 | 고속국도 | 2 |
| 고속국도 | 번화가 | 1 |
| 번화가 | 직장 | 10 |
| 번화가 | 고속국도 | 1 |
이번에 선택된 번화가에서 직장으로 가는 길이 있다! 그런데 직장까지 걸리는 시간이 같아서 손해! 이 경우를 만나면, 이 길보다 고속국도에서 직장으로 가는 길이 더 최적이기 때문에 별다른 업데이트 없이 종료한다.
| 집 | 고속국도 | 2 |
| 고속국도 | 번화가 | 11 |
| 고속국도 | 직장 | 10 |
Tada! 집에서 고속국도까지 2분, 고속국도부터 직장까지 10분 걸리는 경로가 최적의 경로이다!
( 그래프에 양의 가중치를 가진 사이클이 있어서 조금 더 오래 걸렸지만 ) 우리는 최적의 경로를 찾았다!
이게 다익스트라 알고리즘의 핵심이다. 현재 상황에서 가장 최적의 값을 계속해서 업데이트한다!
'Algorithm' 카테고리의 다른 글
| [Data Structure] Trees - 트리구조 (0) | 2020.09.16 |
|---|---|
| [Algorithm] N-Queens, N 퀸즈, N개의 여왕, N 여왕 (0) | 2020.09.15 |
| [Data Structure] Graph - 그래프 (0) | 2020.09.14 |
| [Algorithm] BFS, DFS - 너비우선탐색, 깊이우선탐색 (0) | 2020.09.13 |
| [Data Structure] Hash table - 해시테이블, 객체 (0) | 2020.09.12 |