
문제설명
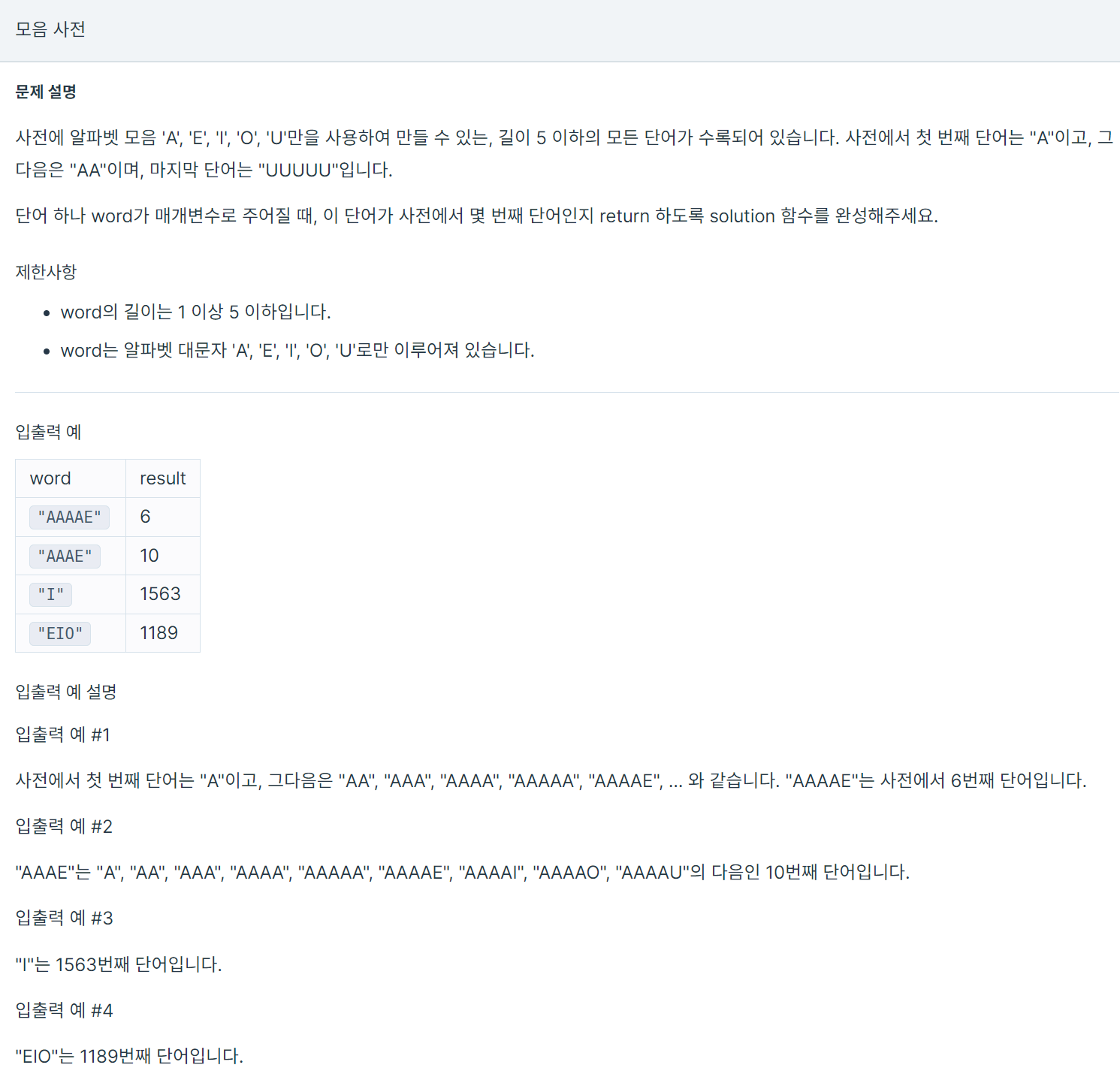
문제분석
지금까지 업로드한 코테 문제는 전부 완전 탐색 카테고리에 포함되어 있습니다. 그래서 당연히 이 문제도 완전 탐색일거라 생각했는데... 왠걸요. 이 문제는 일반항을 구할 수 있으면 훨씬 간단하게 풀 수 있는 문제입니다.
먼저 이 문제는 제한 조건이 있고, 일련의 규칙을 갖는다는 게 어렴풋이 느껴집니다. 그럼 뭐 별 수 있나요. 머리로 하든 손으로 하든 규칙을 찾기 위한 노가다 시작입니다. 먼저 가장 작은 경우부터 확인합니다. 맨 마지막(5번째) 자리의 모음의 인덱스가 커지려면 카운트가 1씩 늘어납니다. 그 다음은 4번째 자리의 모음의 인덱스가 커지는 경우입니다. 가장 마지막 자리의 모음 인덱스가 전부 존재하는 경우는 5가지이고, 존재하지 않는 경우 1가지를 더해 총 6가지가 존재합니다. 뭔가 느낌이 오는 거 같습니다. 3번째 자리도 해보겠습니다. 4번째 자리가 6개 존재할 수 있고, 5번째 자리가 1개 존재할 수 있으므로, 3번째 자리의 인덱스가 커지는 경우는 4번째 자리의 인덱스가 커지는 각 경우의 총합(6 * 5; 6가지 * 모음의 수 5개)은 30이고, 4번째 자리와 마찬가지로 4, 5번째 자리가 없는 경우 1가지를 포함하여 총 31가지가 됩니다. 여기서 어느정도 규칙성을 찾을 수 있습니다.
역시 노가다는 쉽지 않습니다. 예시로 풀어서 써보자면 다음과 같습니다.
- 5번째 자리의 인덱스가 커지는 경우 => 1
- A -> E -> I -> O -> U (1)
- 4번째 자리의 인덱스가 커지는 경우 => 6
- A_ -> AA -> AE -> AI -> AO -> AU (6)
- 3번째 자리의 인덱스가 커지는 경우 => 31
- AA_ -> AAA -> AAE -> AAI -> AAO -> AAU (6)
- AE_ -> AEA -> AEE -> AEI -> AEO -> AEU (6)
- AI_ -> AIA -> AIE -> AII -> AIO -> AIU (6)
- AO_ -> AOA -> AOE -> AOI -> AOO -> AOU (6)
- AU_ -> AUA -> AUE -> AUI -> AUO -> AUU (6)
- A__ (1)
같은 방식으로 접근해서 2번째 자리와 첫번째 자리를 구하면 되는데, 모두 쓰면서 하는 건 너무 빡셉니다. 계산을 통해서 구해보자면, 두번째 자리의 모음의 인덱스가 커지는 경우는 3번째 자리의 인덱스가 커지는 경우 총 5가지에, 3번째 자리의 모음이 없는 경우 1가지를 더해 156((31 * 5) + 1)가지로 구할 수 있습니다. 마찬가지 방식대로 계산하면 첫번째 자리는 (156 * 5) + 1 = 781이 됩니다. 이걸 조금 더 자연스러운 이해를 위해 작은 숫자부터 재정렬 후 일반항을 정리하면 다음과 같습니다.
- f(1) = 1
- f(2) = 6 = f(1) + 5
- f(3) = 31 = f(2) + 5^2
- f(4) = 156 = f(3) + 5^3
- f(5) = 781 = f(4) + 5^4
그리고 위 식을 일반항으로 정리하면 다음과 같습니다.
- if f(1) = 1이고, x가 2보다 크거나 같고 5보다 작거나 같은 자연수일 때,
- f(x) = f(x-1) + 5^(x)
자릿수와 위 일반항의 x는 반대로 정렬돼있으므로 코드로 작성할 때에는 781부터 작성하도록 합니다. 문제를 단순화 했으니 이해하기 쉽게 코드를 짜보겠습니다.
이해하기 쉽게 코드작성하기
function solution(word) {
var answer = word.length;
const gathers = "AEIOU";
const maxNums = [781, 156, 31, 6, 1];
for(let i = 0; i < word.length; i++) {
// 첫번째 자리부터 탐색하며, 각 자리의 몇번째 요소인지 탐색
const idx = gathers.indexOf(word[i]);
// 각 자리의 n번째 요소는 그 앞에 (n-1) * maxNums 개의 경우의 수를 가짐
answer += idx * maxNums[i];
}
return answer;
}for문을 통해 word의 각 자리를 탐색합니다. 이때 현재 자리를 가리키는 word[i]가 모음 순서(AEIOU) 중에서 몇번째(n)인지 확인합니다. 만약 word[i]가 0번째 즉, A라면 A 앞에는 어떤 모음도 올 수 없으므로 idx도 0이고 당연히 그 곱도 0이 됩니다. 만약 word[i]가 O라면, O 앞에 존재하는 AEI 세가지 경우와 현재 자리에 가능한 경우를 곱한 값이 word[i] 까지의 모음의 인덱스가 커지는 경우의 수입니다.
예를 들어서 보자면 다음과 같습니다.
- word === "AAAAE"
- i === 0, word[i] === "A" 일때 => idx === 0, maxNums[i] === 781
- i === 1, word[i] === "A" 일때 => idx === 0, maxNums[i] === 156
- i === 2, word[i] === "A" 일때 => idx === 0, maxNums[i] === 31
- i === 3, word[i] === "A" 일때 => idx === 0, maxNums[i] === 6
- i === 4, word[i] === "E" 일때 => idx === 2, maxNums[i] === 1
- word의 길이가 5자리이므로 각 자리에 모음이 존재하지 않는 경우 총 5가지를 더한 결과는 6
- word === "EEO"
- i === 0, word[i] === "E" 일때 => idx === 1, maxNums[i] === 781 => 781
- i === 1, word[i] === "E" 일때 => idx === 1, maxNums[i] === 156 => 156
- i === 2, word[i] === "O" 일때 => idx === 3, maxNums[i] === 31 => 93
- word의 길이가 3자리이므로 각 자리에 모음이 존재하지 않는 경우 총 3가지를 더한 결과는 1033
간만에 수학적 노가다를 했더니 재밌네요 ㅋㅋ 다음에는 어떤 문제를 업로드할지 기대됩니다.
'Practice for coding test' 카테고리의 다른 글
| 프로그래머스 - Level 1. 행렬의 덧셈 / JavaScript (js) (0) | 2023.02.13 |
|---|---|
| 프로그래머스 - Level 1. 둘만의 암호/ JavaScript (js) (0) | 2023.02.11 |
| 프로그래머스 - Level 1. 개인정보 수집 유효기간 / JavaScript (js) (0) | 2023.02.10 |
| 프로그래머스 - Level 2. 전력망을 둘로 나누기 / JavaScript (js) (0) | 2023.02.08 |
| 프로그래머스 - Level 1. 최소직사각형 / JavaScript (js) (0) | 2023.02.06 |